Research

Active Nematics and Topological Defects

Active nematics are composed of elongated active units that organize in ordered states with nematic symmetry. Although active, these fluids, unlike their polar counterparts, go nowhere on average. Activity, however, drives spontaneous flows and a spatiotemporal chaotic dynamics accompanied by the proliferation of topological defects that has been named "active turbulence". The number of experimental realizations of active nematics continues to grow, spanning inert systems such as vibrated layers of granular rods, in vitro suspensions of cytoskeletal filaments and motor proteins, and living systems such as monolayers of epithelial cells.

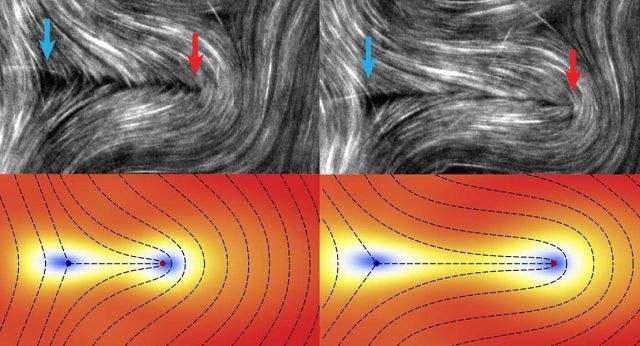
Opposite-sign Defect Pairs Seemingly "repel"

In active nematics the comet-shaped +1/2 defect becomes a motile particle. Thanks to this active motility, the +1/2 defect can overcome the Could attraction to its -1/2 counterpart, so that opposite sign defect pairs seemingly "repel". Top: microtubule bubble suspension imaged in the Dogic Lab. Bottom: theory.

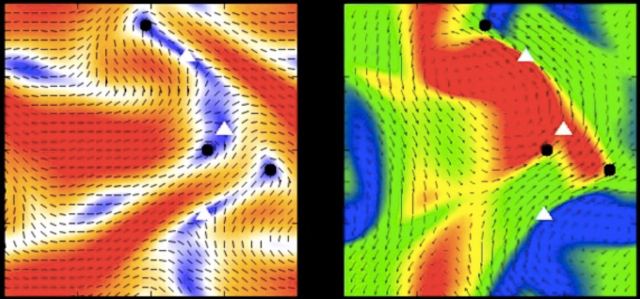
"Active Turbulence"

The numerical solution of active nematic hydrodynamics reproduces the chaotic and self-sustained spatiotemporal dynamics seen in experiments.

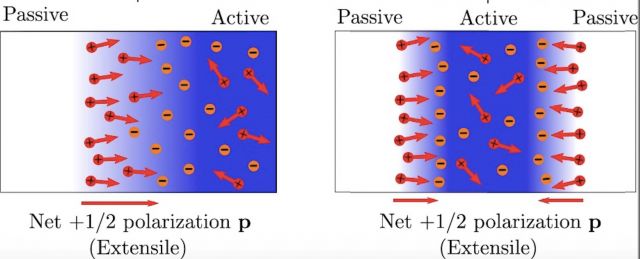
Trapping Defects With Activity Gradients

Due to their motility, the +1= 2 defects accumulate at active-passive interfaces. Activity gradients can be used to sort and guide defects and control active flows. Our hydrodynamic treatment of a gas of active defects provides a versatile framework to address fundamental questions of defect organization in active matter and paves the way for the design of active devices with targeted transport functionalities through the controlled variation of activity.

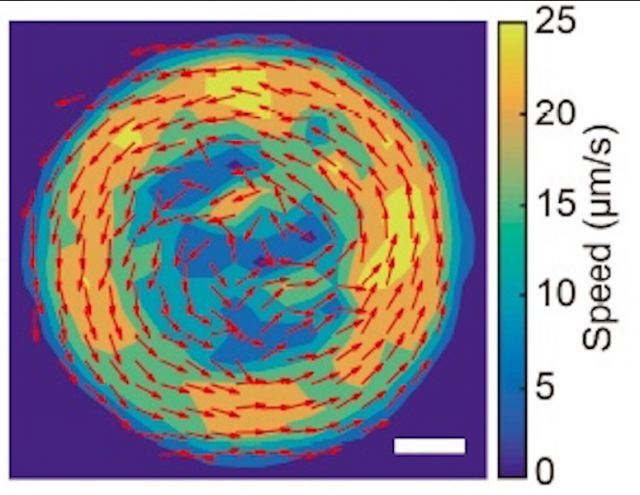
Aggregation and Pattern Formation in Bacterial Collectives

Swimming and gliding bacteria are examples of polar active systems that can organize in complex structures. Our group is interested in disentangling the role of biochemical signaling and chemotaxis from that of physical interactions and interactions and crowding in driving pattern formation.

Effect of Solvent Viscoelasticity on Bacteria Organization

Although in nature most bacteria swim in viscoelastic fluids, the role of viscoelasticity of the suspending fluid on bacterial dynamics is largely unexplored. With experimental collaborator Yilin Wu of the Chinese University of Hong Kong, we are exploring how solvent viscoelasticity affects pattern formation in dense bacterial suspensions.

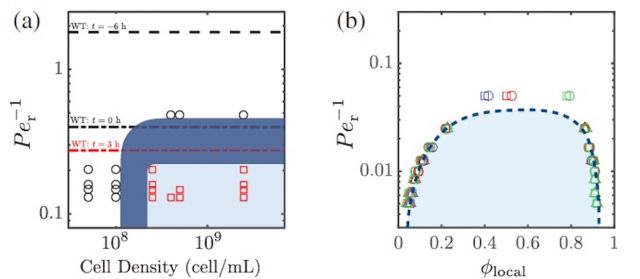
Aggregation of Myxococcus xanthus as a Self-driven Phase Transition

M. xanthus is a rod-shaped, soil-dwelling bacterium that, when starved, organizes into macroscopic, multicellular aggregates known as “fruiting bodies”. Working with the experimental group of Josh Shaevitz at Princeton University, we are using experiments and simulations to investigate the mechanical aspects of fruiting body formation by consider the role of crowding, alignment and reversal in models of reversing Active Brownian Particles and active rod nematics.

The Nonequilibrium Statistical Physics of Active Matter

Active matter, in contrast to equilibrium systems, breaks time reversal symmetry (TRS) at the microscale by continuously dissipating energy locally [5]. Understanding collective effects and fluctuations in active and living matter, even in steady state, therefore requires us to rebuild statistical mechanics to describe a world where detailed balance fails and the microdynamics lacks TRS. We are using minimal models of active matter to address a number of general questions. Can we classify the phases of active matter and characterize these phases by constitutive equations? Are there model active systems that can be mapped onto driven passive ones? Given the profound effects of confinement on active systems, what is the relation between materials properties defined and calculated in bulk active matter and quantities measured in experiments?

Motility-Induced Phase Separation

Purely repulsive active particles with fixed propulsive speed and direction of motion randomized by rotational noise spontaneously phase separate into a dilute gas and a dense phase. This phenomenon is a sort of traffic jam that arises when self-propelled particles slow down due to crowding. It has relevance to bacterial aggregation and assembly of active colloids.

What controls the interfacial tension in MIPS?

When calculated in terms of pressure differences, the interfacial tension is found to be negative. Yet, the interface is stable, although strongly fluctuating.

Active Matter on Curved Surfaces

Flocking, defined as the self-organized ordered motion of collections of self-propelled units, has been the flagship of active matter. Collective cellular motion on curved surfaces is ubiquitous in developmental processes, such as morphogenesis and embryonic development, or when cells migrate in the gut or on the surface of the growing cornea. On a curved geometry, orientationally ordered polar flocks exhibit topological protected edge modes akin to edge states in electronic quantum Hall systems. An open question is weather biology may use topological protection for robust information transport.

Structure and Mechanics of Biological Tissue

Living tissue are active materials with behavior controlled by cell-cell interactions and the interactions of cells with their environment. We use a combination of continuum theory and mesoscopic model to understand collective cell behavior, from coherent migration in wound healing to the selection of shape in development.

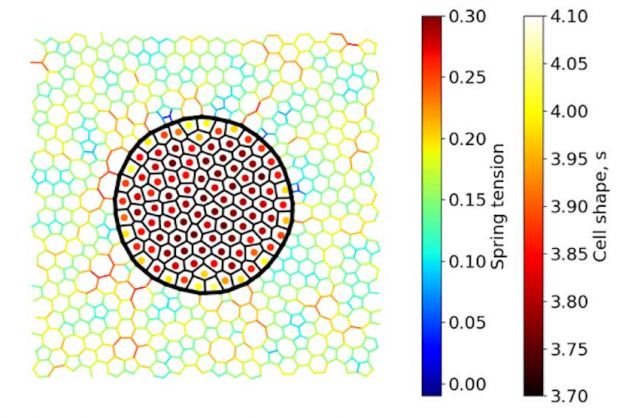
Simulating the Mechanical Coupling Between a Tumor and its Extracellular Matrix

Tumors are surrounded by networks of macromolecules that compose the extracellular matrix (ECM). In collaboration with Lisa Manning and Jen Schwarz of Syracuse University, we use a computational model to explore mechanical interactions between a tumor and its ECM may promote changes in tumor rigidity and morphology and ECM rigidity and structure.

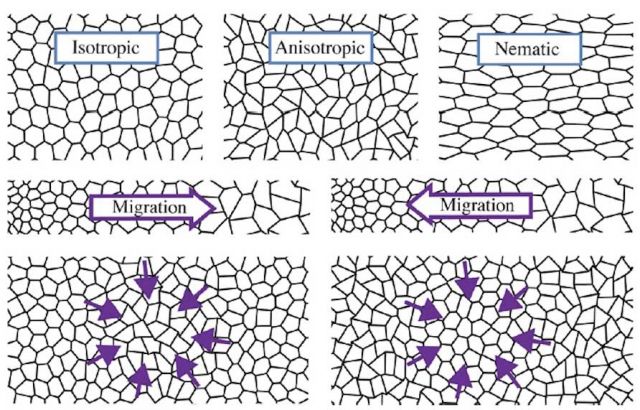
Cell Shape Tunes Rigidity Transitions in Motile Tissue

In biological tissues, mechanical cues are a powerful mechanism for pattern regulation.Such patterns are often described as driven by the expression of chemical morphogens. Using continuum theory we are exploring alternative or complementary purely mechanical mechanisms for tissue sorting and pattern formation.

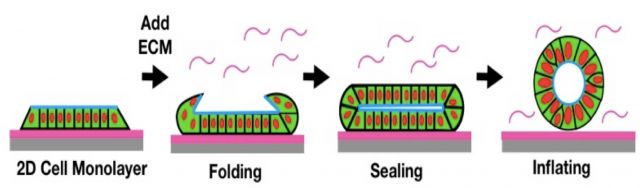
3D Shapes from 2D Sheets

3D biological structures are often achieved by first assembling cells into 2D tissue layers that then attain the desired form of 3D organs and organisms through targeted and repetitive active folding processes. Working with the experimental group of Sebastian Streichan, we combine in vitro experiments with theoretical modeling to understand new modes of folding.